An aesthetic simulation of light refraction.
Abstract
This project employs object-oriented programming in p5.js to create an interactive and visually engaging simulation of light refraction through prisms. Multiple light beams with varying directions are rendered on the canvas, and users can translate and rotate a prism to intersect with the beams, producing refracted light. Due to the different indices of refraction for individual wavelengths, the refracted light separates into a spectrum of colors, forming a rainbow-like visual effect. By applying principles of optics and precise mathematical calculations, the system accurately determines the refraction angle for any given incident angle.
While scientific simulations often prioritize accuracy and clarity, and artistic works frequently emphasize expressive freedom, the dialogue between these two approaches is not always fully explored. This project seeks to bridge artistic expression and scientific reasoning by treating physical laws not as constraints, but as generative structures for visual design. Through this integration, the project aims to support a deeper understanding of optical phenomena while simultaneously inviting viewers to appreciate the aesthetic richness that emerges from physically grounded systems.
Live Demo
Instruction: Press to rotate the prism.
Process
1. Design and composition
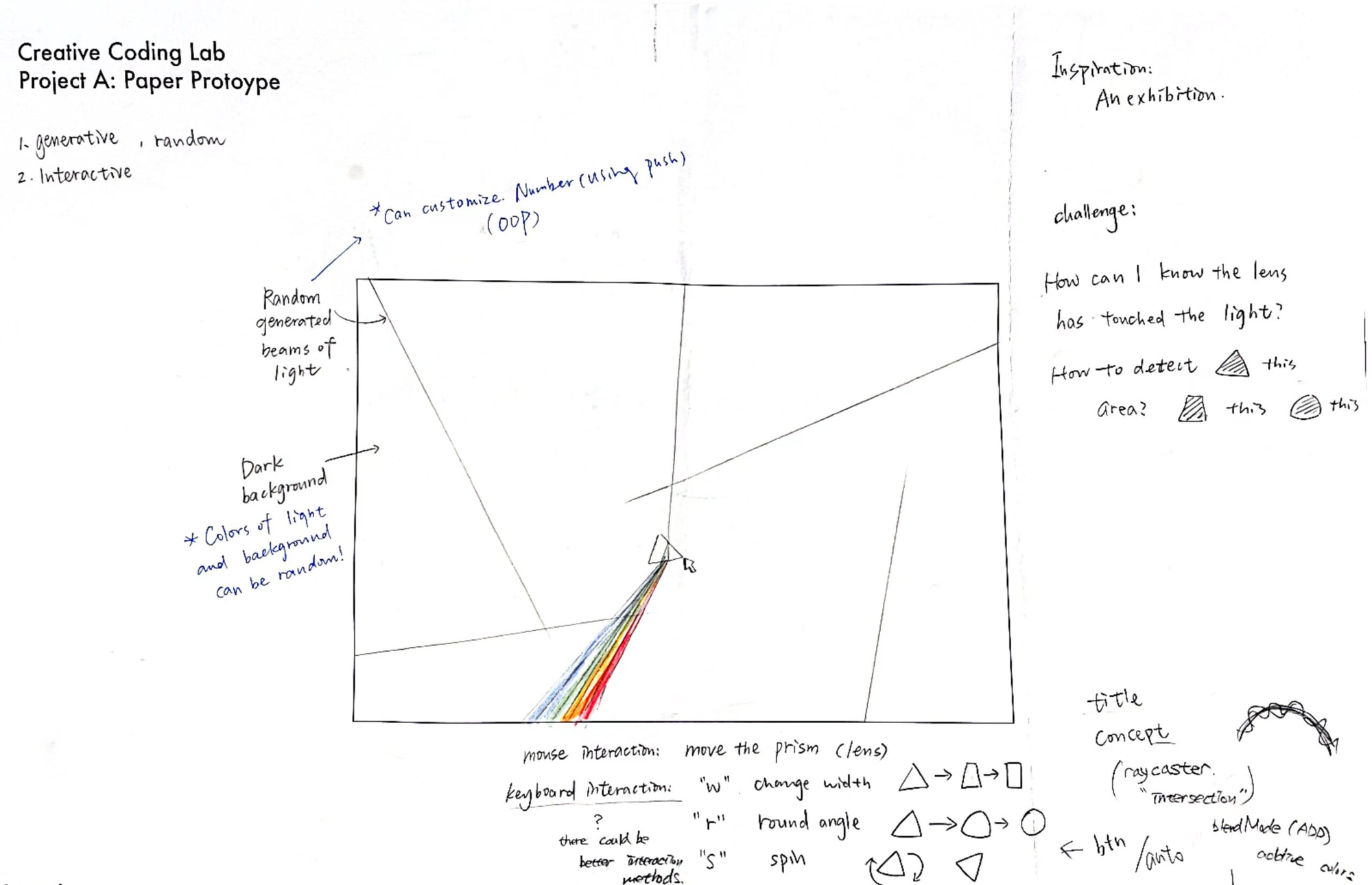
2. Technical Development
Firstly, I analyzed what refraction and reflection lines I should draw, and learned about how to calculate the refraction angle.
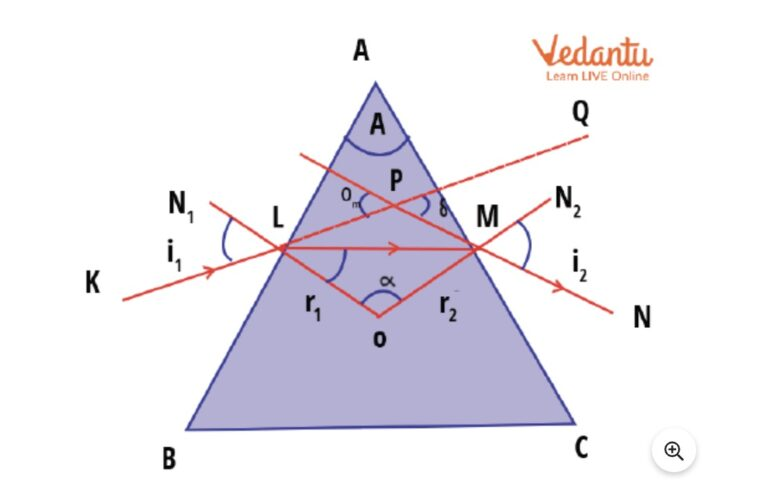
This graph best describes the process of the calculation. It shows that we need to know the normals of line AB and AC, the angle of A, the incidence angle i1, and the refraction index to calculate the emergence angle.
After knowing about the formula and essential variables to calculate the angle, I then have to transform them into what we can operate on in p5js. In other words, it's useful for me to build some classes and create corresponding instances, so that I can set the attributes of the instance and apply the formula to them. The object-oriented programming will make the code more reuseable and can be generally applied.
I decided to first write a test program to test the case that one light beam intersects one prism. The angle of the light beam was set to zero degree to simplify the case.
How to calculate the intersection of two lines (or one line and one ray)? Prof. Moon suggested watching the 2D raycasting by the Coding Train to me and that video helped me a lot. It not only helped me with calculating the intersection point, but also inspired me of using a framework of object-oriented programming to build my project.
Inspired by the video, I created 2 classes at first: The Prism class and the Beam class. The Prism class consists of 3 vertices of the prism so that the 3 surfaces of the prism can also be calculated through the 3 vertices.

And then I realized an issue. By knowing the vertices and their corresponding lines, I can calculate the intersection points. However, when I want to rotate the prism, if I simply use the rotate(angle) function and the push(), pop(), it only rotates the visual representation of the line, but doesn't actually rotate its position in the coordinate, so that the calculation of the intersection point was not applicable when the prism is being rotated. Therefore, I searched for methods to rotate the positions of the vertices themselves. Sounds like the rotation matrix can help me do this.

Source: https://www.cuemath.com/algebra/rotation-matrix/
Another challenge was that there are two refractions in the process. The first one happens inside the prism with the refraction index larger than 1 (rarer to denser), and the second one happens outside the prism with the refraction index smaller than 1 (denser to rarer). Since the two have something in common and I have already wrote a lot of code for the first refraction, I would really like to reuse the code when calculating the second refraction. To do this, I created another Beam instance from the first intersection point so that it can calculate the second intersection point with the second surface automatically. I guess this uses some concepts of recursion.
Try this demo for the optical effect of a prism.
One helpful thing for this situation is to clear my code from the beginning and unify some measurements. For example, we can see that in the case of zero degreed light beam, the only possible angle of incidence lies in (-PI/2, PI/2), and if I discuss it by 2 classifications, the angle of incidence will lie in (0, PI/2) under a narrower condition. However, when the angle of the light beam is changed, this way of calculation is not useable anymore. Therefore, I tried to unify the measurement of angles in many ways, and failed several times.
One way that I spent much time on was to transform all the angles to (-PI/2, PI/2). It's because the tangent value is unique when the angle is limited to (-PI/2, PI/2). However, after several attempts, I found that it's still not applicable for all cases. I also tried the (0, 2PI) measurement but found that it is making the situation too complicated.
Therefore, I thought from another angle. If only changing the measurements does not work out, then we have to adjust the way class instances are arranged. I realized that the difficulty was there because the class instance doesn't store enough information for me to get the calculation done easily. Therefore I added another class, Surface, which keeps track of the three surfaces of the prism and also, the vector direction of their normals, and the prism vertex at its opposite side. In addition, I eventually decided to unify the angles to (0, 2PI) because it works best for the calculation.
Appendix
Resources that helped me with understanding the principle of light refraction:
