Make Van Gogh's Starry Night move through a flow field system.
Abstract
This project animates Van Gogh's Starry Night by implementing a particle-based flow field system in p5.js. Inspired by Karl Sims' vortex field research, I developed an algorithm that creates swirling movements through Perlin noise and tangential forces. The system allows users to interactively paint vortex centers or automatically detects star positions from the original painting through RGB color analysis. By combining flow field dynamics with pixel manipulation, the project transforms static paintings into flowing, dynamic visualizations that enhance the sense of motion, energy, and flux originally conveyed through Van Gogh's brushwork.
Toolkit
p5.js
Trailer Video
Process
A. Concept
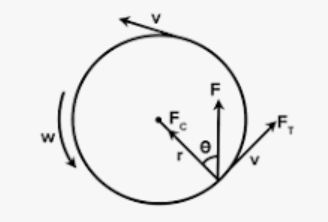
I was attracted by this image when reading the article "Particle animation and rendering using data parallel computation" by Karl Sims:

This vortex field (or swirling pattern) reminds me of Starry Night by Vincent van Gogh. He created a strong sense of motion, energy, and flux through the use of brushwork and colors.

There are many other examples that the static 2D paintings are trying to convey a sense of movement. I think it would be great if I could enhance this message to the audience by animating these drawings. Therefore, I decided to create a "moving" version of Starry Night for my midterm project using the flow field and the particle system.
B. Implementation
Here are the questions to solve to achieve my goal of creating a flowing painting.
- Swirling movement of the particles
- Location of the center
- Aesthetics of the strokes
1. Swirling movement of the particles
Firstly, I need to know how to make the particles move in a circular pattern. The particles need to be placed in a flow field that they will be given the velocity according to their position in the field. However, there are different kinds of flow fields: Perlin noise flow fields, vortex flow fields, magnetic flow fields, and so on. I searched the Internet and found a simple way of creating this swirling effect.

Basically, you create a background image showing the distribution of the centers of vortices based on a 2D Perlin noise space. And then you calculate the "pressure differential" around every cell in the grid. That differential vector will point to the center of the vortex, creating an attraction effect to the particles. However, if you rotate every vector by 90 degrees, they will suddenly be turned to some force similar to the "tangential force". This will magically turn the movement of the particles into a swirling pattern.
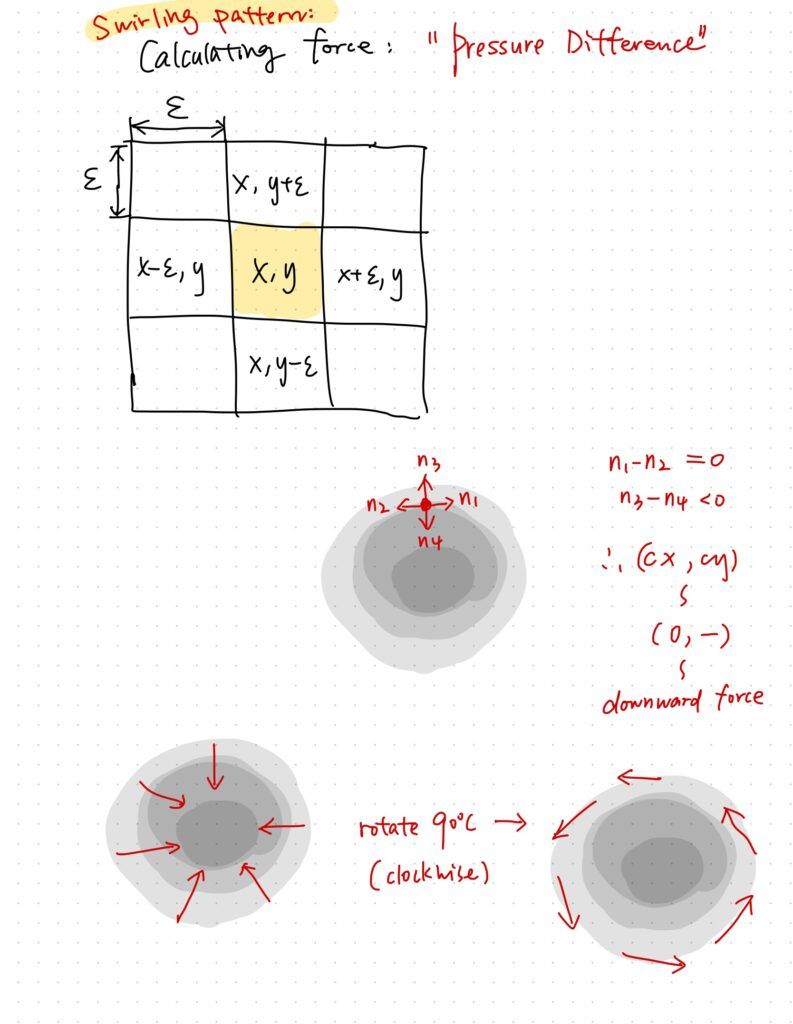
Generating a flow field with Perlin noise is a good starting point.
p.s. Here's a good way of modifying the noise field to make it cleaner and less "noisy". You can change the parameters in this function called noiseDetail(octave count, falloff).


I also make a 3D noise field that changes through time.
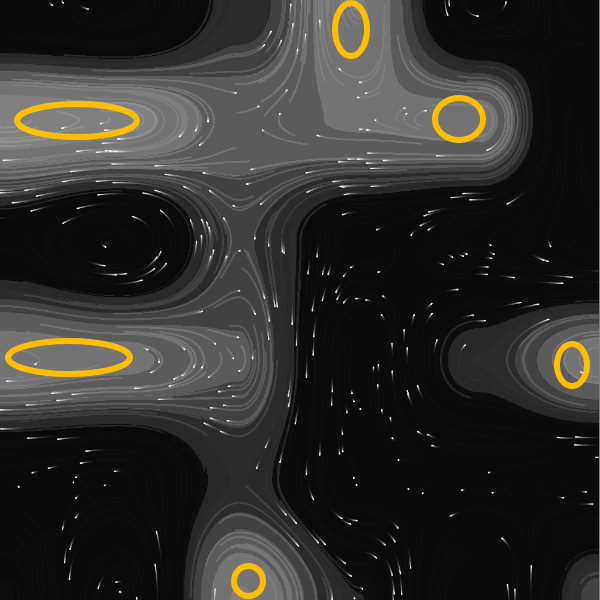
Here are some generative patterns I created from the swirling field:





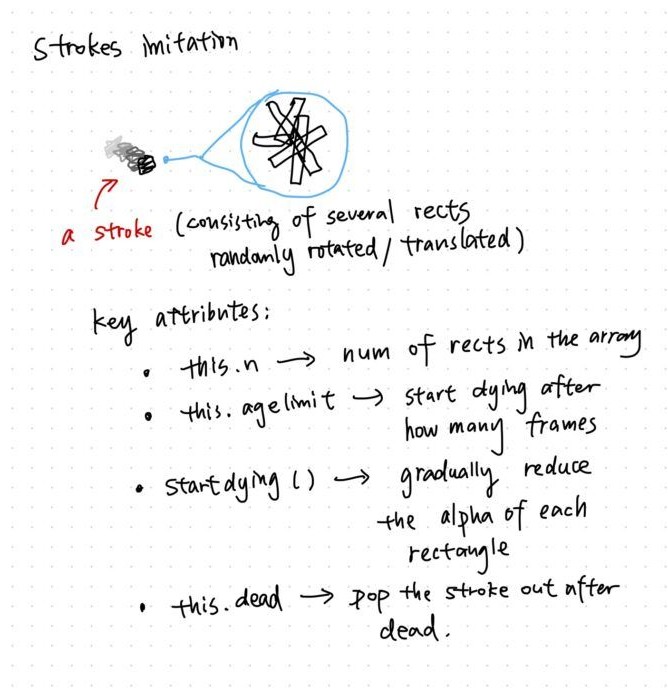
I also made this blinking effect. The explanation is in the image.
2. Location of the center
Then, we need to know the rotation center of the stars.
In the previous sketches, I used the Perlin noise field to determine the rotation centers. Every time, the resulting image is different because of the difference in random Perlin noise.
However, the Perlin noise is too random and you can't really decide where your centers are. Therefore, I came up with the idea of allowing the users to paint on a buffer canvas and have control over their center locations.
The method is to use pixel manipulation.
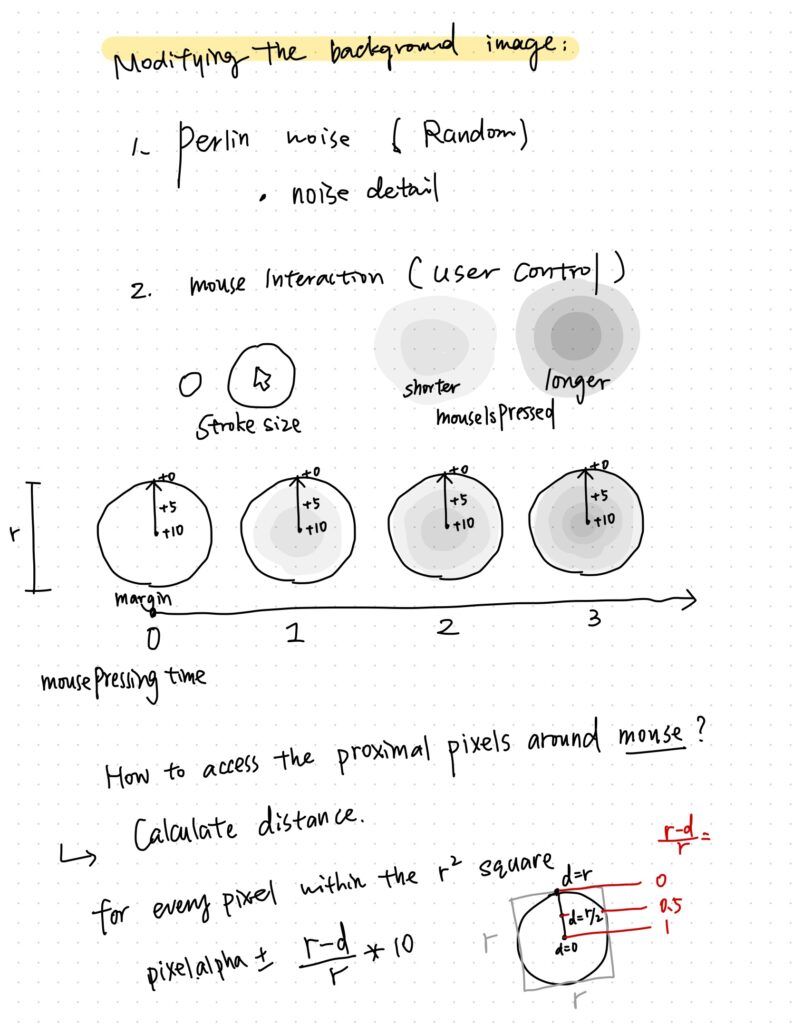
I wrote a function called renderImg() that modifies an initially pure black buffer canvas. Whenever the users press their mouse, the pixels around the mouse position will gradually turn brighter according to their distance from the mouse position.

(A clearer demonstration)
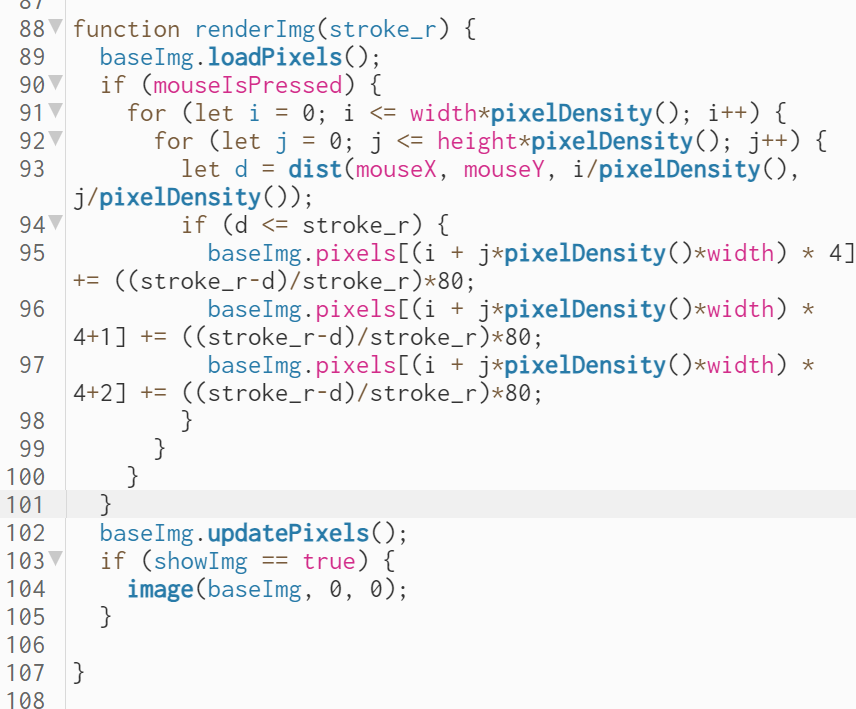
Then, the users will be able to draw their own "base image" in the field and affect the movement of the particles.

Do you want to have a try? (press i to show your base image)
Some result:


Lastly, apart from user modification, I also want to "animate" the original painting by Van Gogh. This requires us to take the original painting as the source image.
But how can the computer know the locations of rotation centers of the stars from the painting?

At first, I tried to detect the pixels that have a higher grey scale (brighter). But as you can see, there is only one star that is statistically much brighter than others. This method didn't work well.
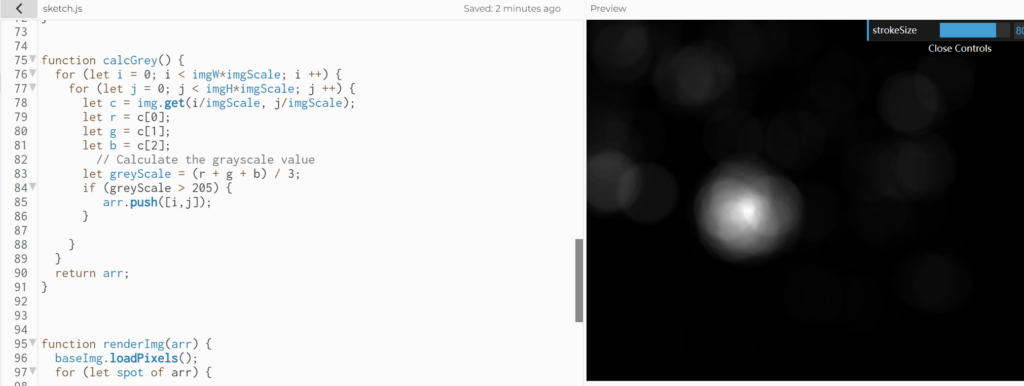
Then I noticed that all the stars are kind of yellow. Therefore, I thought of calculating the Euclidean distance of the RGB value of the pixel with the RGB value of a "standard yellow color". After some tests, I found that this rule works the best (but still not perfect) anyways I tried...
abs(r-g)<=20; r: 180 += 20; g: 165 += 20; b: 60 += 30;
And then I used the previous renderImg() function to render the base image based on the original painting. You can see that nearly half of the stars have been detected.

Finally, I combined the Perlin noise flow field with this swirling field. Adding some dynamics to the sketch. I also grabbed the original color from the painting and modified the color of the pixels.
